Ruby Cubes

04 Oct 2006

The 6 Pieces

At a recent get-together with friends, I found myself playing with a wooden puzzle consisting of 6 pieces that were claimed to be able to come together to form a solid cube.

Lucy, the puzzle’s owner, said she had owned it for years and never successfully solved it. Not to be detered, I spent the whole evening failing to get anywhere with it.

Continuing not be detered, I decided to do the honorable geek thing and write a computer program to solve it.

Herewith how I approached the problem and got started with ruby.

Investigating the problem

I decided early on to go for an educated brute-force approach; educated in the sense that there were bound to be some assumptions that I could make to simplify things. To get a sense of the full scale of the problem, I wanted to calculate the number of combinations that the pieces could be arranged in.

Consider each piece to consist of a number of 1x1x1 cubes and that there is a key cube within each piece. The key cube of each piece can be located in one of the 3x3x3=27 different locations in the solution cube (aka box). Each piece can then be rotated to 24 different orientations. This leads to having 24*27=648 arrangements of just one piece. We could crudely say this leads to 648^6 arrangements of all six pieces - 74,037,208,411,275,264.

However, once the first piece is placed, we know that the key cube of the second piece cannot be located in the space the key cube of the first piece is. This means there are 27*26*25*24*23*22=213127200 arrangements of the pieces with regard position only. To factor in rotation, as there is no dependency between piece’s rotation, there are 24^6=191102976 arrangements of the pieces. Combining these gives: 213127200*191102976=40,729,242,186,547,200 combinations. Whilst not an order of magnitude less than the previous value, the figure is headed in a good direction.

However, even if these combinations were to be consided at 1000 per second, it would take over 1291515 years to complete. It’s clear there needs to be some further refinement to the problem.

The trick to simplifying the problem is realising that we do not need to consider every combination of every piece. To see this, the constraints that describe a ‘good’ placement of a piece need to be defined:

1. The piece must fit entirely within the 3x3x3 box
2. Once placed, the piece must not leave any voids in the solution cube that are 3 or less cubes in size (as all of the pieces consist of at least 4 cubes)

Given a partial solution that has 2 pieces currently placed, if we find it impossible to place the third piece into the box without violating any of the constraints then it is not worth even trying to place any of the other 3 pieces. By considering each piece in turn like this, it is possible to make life even easier by considering the more complex pieces first - ie the ones with 5 cubes in them.

The next simplification comes by considering the arrangements of the very first piece; we have already decided that it will be a 5-cube piece. All such pieces are 3-cubes long in one of the axis - in other words, the key-cube of the piece can be moved in only 2 axis; moving it in the third axis would lead to the piece not fitting entirely in the box - violating the first constraint.

Furthermore, it is not necessary to consider any of the rotations of the first piece. This comes from the fact that we could just as easily rotate the box around a fixed first piece and get to an equivalent arrangment. Armed with these facts, it can be seen that a well-selected first piece only has 4 potential positions - that is 2 orders of magnitude less than the originally quoted 648 positions.

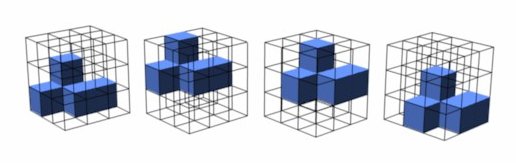
The four positions for piece one

Enough of the theoretical.

Implementing it in ruby

Some of the problems that had to be solved include:

• Representing the box and pieces
• Rotating the pieces
• For a given location in the box and rotation on each axis, does a piece fit?
• For a given location in the box and rotation on each axis, actually placing a piece
• Checking the box is ‘ok’ - whilst a piece may fit in the box, if it leaves a 3 (or less) cube void then the box is not ‘ok’
• Iterating over the pieces
• Detecting that a solution has been reached

Representing the box and pieces

I decided to represent the box as a multi-dimensional array:

box = [[[0,0,0],
            [0,0,0],
             [0,0,0]],
          [[0,0,0],
            [0,0,0],
              [0,0,0]],
          [[0,0,0],
             [0,0,0],
              [0,0,0]]]

A 0 represents an empty space in the box. Any other value represents piece number occupying that spot.

The pieces are represented in a hash, indexed by the piece number, with the cubes of each piece listed as offsets from the key-cube.

pieces = {
   1 => [[0,0,0],[0,0,1],[0,1,1],[1,0,1],[1,0,2]],
   ...
}

Rotating the pieces

This led me to re-learn some basic geometry to do with rotation matrices. Given a matrix M representing a point in space and a matrix R representing the rotation to be applied, the resultant point is simply the product of the two. Ruby comes in very handy here as a simple require 'matrix' gave me all the matrix functionality I could wish for.

To help with the efficiency of the program I implemented a simple caching function that meant I didn’t have to perform the multiplication every time a particular rotation was needed. I didn’t do any quantative measurements of what gain this gave, but it felt good to do.

Checking a piece fits

For each cube in the piece, I knew its offset from the ‘origin’ location. If this location was outside of the box (ie <0 or >2) then the piece didn’t fit. If the location was already occupied (ie non-zero in the box array) then, again, the piece didn’t fit.

Placing a piece

Assuming the piece fits, placing it in the box is simply a question of iterating over its cubes and updating the box array in the appropriate locations to the piece number.

Checking the box is ‘ok’

Whilst the constraint to be checked is that there are no voids of 3 cubes or less, I found it was far easier to initially check for 1 cube voids. This is done by checking each cube in the box that is empty and seeing whether it has an empty neighbour - if so, it is ‘ok’ in this looser definition of the constraint.

Iterating over the pieces

I wrote a function that, for a given position and rotation, finds the next location for the piece by iterating over the remaining positions and rotations. To do this I defined a natural ordering of these properties so that locations are iterated over prior to rotations.

If the function finds a suitable placement for the piece it returns an array of the position and rotation of the piece. This allows the code to store these values on a stack and progress to the next piece to try and place it in the current box.

If the function fails to find a placement it returns an empy array that triggers the code to step back to the previous piece, obtain that piece’s current position and rotation from the stack and call the placement function with these values so the next location can be found and evaluated.

This recursive method required the most thought, debug and rewriting.

Detecting a solution

I ended up implementing a number of checks for a solution in paranoia that I had got a piece of logic wrong somewhere. One involved counting the number of pieces successfully placed into the box - once all were placed, a solution would have been found. Another was within the function to check the box for voids of appropraite size; if it found no voids whatsoever, then by definition the box is complete.

Clearly there are plenty of implementation details I am leaving out here. The logic of the approach has been covered, which ought to be enough and is frankly the more interesting part.

Finding the solution

It is only fair to point out that I didn’t do a full pen and paper analysis of the problem before I started coding. This is demonstrated by the fact that the first version of the code ran for hours on end without getting anywhere. The single biggest efficiency saver was the code to detect one-cube voids in the current partial solution - this led to it taking minutes to cover ground it had previously taken all night to do.

To help track it’s progress I had the code report how many positions it had considered for each piece. The theory was that the code should not have to consider any more than 4 positions for the first piece. However the code was getting to the 5th position for the first piece without a solution being found. This led me to find and fix quite a few bugs in the implementation. I also verified that the first positions considered for the piece were actually the right ones.

Even with this, a solution was not being found. I decided to test the program with a set of pieces that I knew had a solution; the Soma cube. It did take a few modifications due to the different number of pieces etc, but it didn’t take long for it to find a solution - which, considering there are 240 solutions to the Soma cube, shouldn’t have been too hard. This helped to validate the overall correctness of the code.

The solution

With this in mind I re-ran the original pieces through the program, but still without a solution being found. At this point I felt safe to declare that there simply is not a solution for this particular set of pieces.

Alternative Pieces

But I wasn’t going to stop there. I decided to investigate whether any of the pieces had been ‘altered’.

Taking each piece in turn I mirrored it and ran it through the program. For two of the pieces, solutions were found.

Going forward

Whilst I have some reasonably generic ruby code that can find solutions to this type of problem there are plenty of next steps that I could take. The first few that come to mind include:

• The existing code is very procedural - barely scratching the surface of what can be done with ruby. The ‘box’ and ‘piece’ concepts of the puzzle do lend themselves to a more object-oriented design and implementation. Ruby certain allows for this.
• The void-constraint checking can be improved to spot the 2- or 3-cube voids.
• The order the pieces were placed into the box was selected by-hand based on my own judgement of piece complexity. It would be interesting to programmatically identify piece complexity

How much I actually do now that I have broken the bad news to Lucy that her puzzle isn’t solvable is another matter.